共时性和历时性区别
共时性(synchronic)和历时性(diachronic)是语言学中用来描述语言研究的两个基本维度。
1. 共时性:指的是在特定时间点上对语言系统的研究,即对语言结构在同一时间层面上的分析。这种研究关注的是语言的静态状态,比如某个时期的语法规则、词汇、音系等。共时性研究不涉及语言随时间的变化,而是将语言视为一个封闭的系统,研究其内部各部分之间的关系。
2. 历时性:与共时性相对,历时性研究关注的是语言随时间的发展和变化。这种研究涉及语言的历史,包括语言的起源、演变、分化以及消亡等。历时性研究可以帮助我们了解语言是如何随着时间而发展变化的,以及不同语言之间的亲缘关系。
简单来说,共时性研究的是语言的“横截面”,而历时性研究的是语言的“时间线”。两者都是语言学研究中不可或缺的部分,有助于我们全面理解语言的复杂性和动态性。
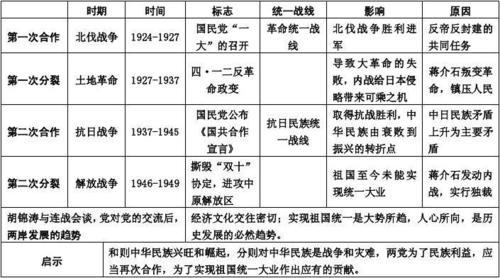
历时性与共时性的概念
历时性(diachrony)与共时性(synchrony)是语言学中两个重要的概念,它们描述了语言研究的两种不同视角。
1. 历时性:指的是对语言随时间变化的研究,即语言的历史发展。历时语言学家会研究语言从古至今的演变过程,包括语音、词汇、语法、句法等方面的变化。历时性研究关注语言的起源、发展、变化以及消亡等历史问题。
2. 共时性:指的是对特定时间点上语言状态的研究,即语言的当前状态。共时语言学家会研究语言在某一特定时期的结构和功能,而不考虑它的历史发展。共时性研究关注语言的静态特征,如音位系统、语法规则、词汇用法等。
这两个概念最早由瑞士语言学家费迪南·德·索绪尔(ferdinand de saussure)提出。他认为,要全面理解语言,就必须同时考虑历时性和共时性两个维度。历时性研究帮助我们了解语言的演变过程,而共时性研究则帮助我们理解语言在特定时期的运作方式。
在实际的语言研究中,历时性和共时性往往是相辅相成的。例如,了解一个语言的历史演变有助于我们理解其当前的语法结构和词汇用法;反之,对当前语言状态的深入分析也可以为理解其历史发展提供线索。
连续性和一致连续性的区别
在数学分析中,连续性和一致连续性是两个不同的概念,它们描述了函数在不同程度上的平滑性质。
连续性
一个函数\(f(x)\)在点\(c\)处连续,如果满足以下条件:
1. \(\lim_{x \to c} f(x)\) 存在;
2. \(\lim_{x \to c} f(x) = f(c)\)。
这意味着,当\(x\)无限接近于\(c\)时,函数\(f(x)\)的值无限接近于\(f(c)\)。连续性通常用于描述函数在某一点的局部行为。
一致连续性
一个函数\(f(x)\)在区间\(i\)上一致连续,如果对于任意的正数\(\epsilon\),存在一个正数\(\delta\),使得对于区间\(i\)内的所有\(x\)和\(y\),只要\(|x - y| < \delta\),就有\(|f(x) - f(y)| < \epsilon\)。
一致连续性比连续性要求更严格,它要求函数在整个区间内的行为都是平滑的,即任意两点之间的函数值差异都不会超过一个给定的界限,无论这两点有多接近。
区别
1. 局部性质 vs 全局性质:连续性是局部性质,只关注函数在某一点的极限行为;而一致连续性是全局性质,要求函数在整个定义域内的行为都是平滑的。
2. 条件:连续性要求函数在某一点的极限存在且等于该点的函数值;一致连续性要求对于任意两点,只要这两点足够接近,函数值之间的差异就可以被任意小的正数\(\epsilon\)所限制。
3. 应用:连续性是微积分中的一个基本概念,而一致连续性在分析函数的全局性质时更为重要,如在证明极值定理或解决一些积分问题时。
简而言之,连续性关注的是函数在某一点的局部行为,而一致连续性则要求函数在整个定义域内的行为都是平滑的。
 微信扫一扫打赏
微信扫一扫打赏